定义

插入排序（英文：insertion Sort）是一种简单直观的排序算法。它的工作原理是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。插入排序在实现上，通常采用in-place排序（即只需用到O(1)的额外空间的排序），因而在从后向前扫描过程中，需要反复把已排序元素逐步向后挪位，为最新元素提供插入空间。

插入排序演示动画1

算法步骤

插入排序算法的运作如下：

  • 从第一个元素开始，该元素可以认为已经被排序
  • 取出下一个元素，在已经排序的元素序列中从后向前扫描
  • 如果该元素（已排序）大于新元素，将该元素移到下一位置
  • 重复步骤3，直到找到已排序的元素小于或者等于新元素的位置
  • 将新元素插入到该位置后
  • 重复步骤2~5

如果比较操作的代价比交换操作大的话，可以采用二分查找法来减少比较操作的数目。该算法可以认为是插入排序的一个变种，称为二分查找插入排序。

伪代码如下：

1
2
3
4
5
6
7
8
9
10
11
insertion_sort(array, length)
{
    var i, j, temp;
    for (i = 1; i < length; i++) {
        temp = array[i]; //与已排序的数逐一比较，大于temp时，该数向后移
        for (j = i - 1; j >= 0 && array[j] > temp; j--) 
            array[j + 1] = array[j];

        array[j+1] = temp; //被排序数放到正确的位置
    }
}

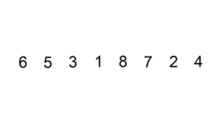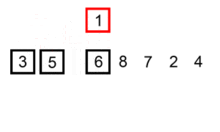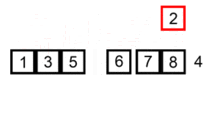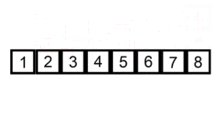
插入排序动画演示2

代码实现（java）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
/**
 * 插入排序的简单实现
 */
public static void insertSort(int[] nums) {
    for (int i = 1; i < nums.length; i++) {
        int value = nums[i];
        int j = i - 1;
        while (j >= 0 && nums[j] > value) {
            nums[j + 1] = nums[j];
            j = j - 1;
        }
        nums[j + 1] = value;
    }
}

算法复杂度分析

如果目标是把n个元素的序列升序排列，那么采用插入排序存在最好情况和最坏情况。最好情况就是，序列已经是升序排列了，在这种情况下，需要进行的比较操作需(n-1)次即可。最坏情况就是，序列是降序排列，那么此时需要进行的比较共有n(n-1)/2次。插入排序的赋值操作是比较操作的次数加上(n-1)次。平均来说插入排序算法复杂度为O(n2)。因而，插入排序不适合对于数据量比较大的排序应用。但是，如果需要排序的数据量很小，例如，量级小于千，那么插入排序还是一个不错的选择。 插入排序在工业级库中也有着广泛的应用，在STL的sort算法和stdlib的qsort算法中，都将插入排序作为快速排序的补充，用于少量元素的排序（通常为8个或以下）。

参考文章